

I've update my original post here with my results. I figured out I was mixing up the scale and the rate parameters, and therefore getting the parameters for my distribution wrong. and I want to get the probability I have to wait between wait between 12 and 8 hours to catch 50 fish → (12, a=50, loc=0, scale=1/5) - (8, a=50, loc=0, scale=1/5) Now, I get a probably (below) which is more in line with expectations.
The average waiting time is 10 hours to catch 50 fish.
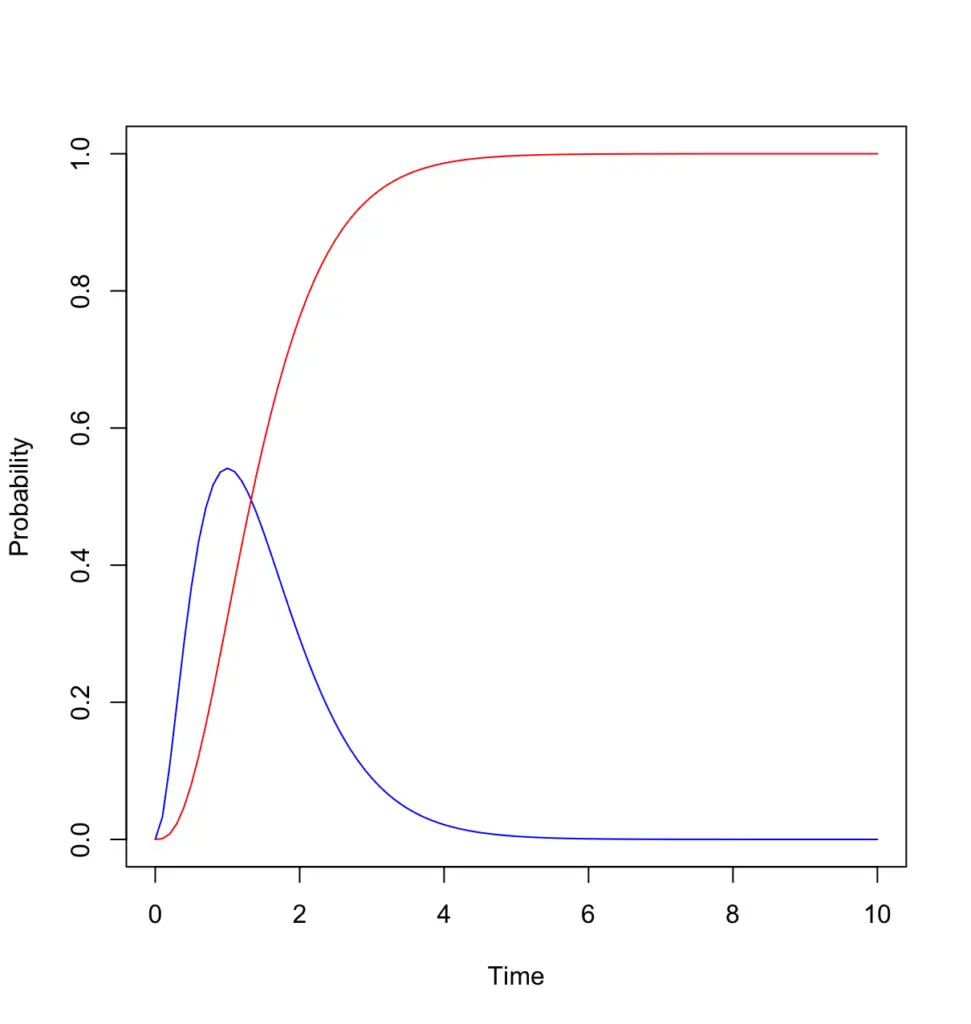
So, if I revise the inputs and choose 1/5 as my scale. As ab increases, the distribution becomes more symmetric, and the mean approaches the median. So I was inputting the scale wrong based on the assumptions to my question. Compute the cdf of the mean of the gamma distribution, which is equal to the product of the parameters ab. which would be inline with my results almost zero for the second example. So in my example 50*10 = 500 hours for waiting time. I believe the intuition is (scale * a) = average waiting time. My original reasoning was if I'm catching on average 10 fish an hour, it would be probable (at least higher than my answer) I would catch 50 somewhere between 4 and 6 hours.Does the above answer seem correct? What is the intuition behind it?.My shape parameter here is 50 (I believe), and I use the same formula from above but with tweaking a few things. And I want to see the probability I have to wait between wait between 4 and 6 hours to catch 50 fish. Say instead of catching 1 fish every half hour, you instead catch 5 fish every half hour so θ = scale = 10 (10 fish on average per hour). Now I wanted to pay with the results and see if I could get answers which were intuitive. I re-created this in scipy and got the same answer import scipy.stats as stats One fish every 1/2 hour means we would expect to get θ = 1 / 0.5 = 2 fish every hour on average. Compute the probability that you will have to wait between 2 to 4 hours before you catch 4 fish. Suppose you are fishing and you expect to get a fish once every 1/2 hour. I'm learning about gamma distributions and I want to make sure my reasoning is correct for an example I found here I posted this question on cross validated, however I wanted to see if I could also get an answer here. R-bloggers - blog aggregator with statistics articles generally done with R software. Kaggle Self posts with throwaway accounts will be deleted by AutoModerator Memes and image macros are not acceptable forms of content. Just because it has a statistic in it doesn't make it statistics. Please try to keep submissions on topic and of high quality. They will be swiftly removed, so don't waste your time! Please kindly post those over at: r/homeworkhelp. This is not a subreddit for homework questions.
#Gamma cdf software#
This is a subreddit for the discussion of statistical theory, software and application.Īll Posts Require One of the Following Tags in the Post Title! If you do not flag your post, automoderator will delete it: Tag
#Gamma cdf how to#
Homework questions are for r/homeworkhelp How to ask a statistics question Modmail us if your submission doesn't appear right away, it's probably in the spam filter.


 0 kommentar(er)
0 kommentar(er)
